Did you know that nearly every electrical device you use—your phone charger, your fridge, even the lights in your home—relies on one specific type of waveform? It’s called the sinusoidal wave, and it’s far more than just a smooth curve on a graph. Many people think electricity is either on or off, but in reality, understanding sine wave signals and how alternating current (AC) works gives you a whole new perspective on how modern power systems function. In this article on the Tech4Ultra Electrical website, you’ll discover how the AC waveform powers your world and why its smooth oscillations are the backbone of our energy infrastructure.

What is a Signal?

A signal is simply a way to represent information. That’s it. Whether it’s a voice over a phone line, the brightness level of your screen, or the speed of your internet—signals are how data travels, transforms, and gets interpreted by systems.

From a technical angle, a signal is a function that varies with time (or sometimes with space), and it carries information. It can be analog, like the smooth fluctuations of sound waves, or digital, like the 0s and 1s your computer processes.

When I first started learning about electronics, the concept of a “signal” felt too abstract—like it was just theoretical fluff. But when I saw a live oscilloscope tracing the voltage from a guitar pickup, it clicked: the voltage was the signal—real, measurable, alive.

Here’s what helps to make sense of it:

Time-based changes: Signals change over time, like the heartbeat on a monitor.
Amplitude: This shows the strength or value of the signal at any moment.
Frequency: How often the signal repeats itself per second.

In short, a signal is the language that electronic devices use to talk to each other and interpret the world.

What is a Sinusoidal Wave Signal?

Now we’re getting to the heart of it.

A sinusoidal wave signal, often just called a sine wave signal, is one of the most fundamental forms of signal in the world of electronics and physics. If you’ve ever seen a smooth, repetitive wave pattern on a graph—like a rolling hill—that’s a sinusoidal wave.

But here’s the thing: it’s not just a pretty curve.

It represents alternating current (AC) in most electrical systems, including the electricity from your wall socket. Why? Because a sinusoidal waveform offers several advantages: it’s smooth, easy to generate, and efficient for transmitting power.

When I first connected a function generator to a speaker and listened to the result, the sine wave sounded pure—like a clean tone. No distortion, no noise—just clarity. That’s why it’s the go-to wave for analyzing systems.

Key features of a sinusoidal signal:

Amplitude: The peak value of the wave.
Frequency: Measured in Hertz (Hz), it shows how many cycles occur per second.
Phase: Indicates the starting angle of the wave.

Why it matters?

It’s the foundation of all AC waveform analysis.
It models natural phenomena like sound, light, and even ocean waves.
It simplifies math: engineers love it because it makes systems easier to understand and predict.

So the next time you see a sine wave, remember—you’re looking at the heartbeat of modern electrical systems.

Why are Sinusoidal Wave Signals Important?

Here’s the deal: sinusoidal wave signals aren’t just common—they’re practically the backbone of signal processing. When I first started messing around with circuits in school, I quickly realized that almost every test signal I was using was a sine wave. There’s a reason for that.

The importance of sine wave signals comes down to their predictability, efficiency, and versatility. Whether it’s the power coming out of your wall or the signal your phone’s antenna is receiving, if it’s electrical and it carries information or power—it probably involves a sine wave.

Here’s why that matters:

Clean Energy Transfer: Alternating current (AC) in power grids is sinusoidal because it’s easier to manage and transform with minimal loss.
Signal Integrity: In communication, sine waves are the most reliable carriers of information, with less distortion and noise.
System Behavior: Many systems naturally respond to sinusoids, so using them as test signals gives the clearest picture of system performance.

And if you ever dive into audio engineering, radio, or radar systems, you’ll find one constant: everything revolves around AC waveforms that look just like sine waves. They’re everywhere because they work—pure and simple.

Why it’s foundational in electrical and communication systems

Let’s not sugarcoat it—without the sinusoidal wave, our modern world would pretty much collapse. It’s that essential. The reason is simple: this wave behaves in a way that’s mathematically predictable and physically efficient.

In electrical systems, the entire concept of alternating current (AC) is based on sinusoidal wave signals. Why? Because they minimize energy loss when power travels long distances through cables. Utilities love sine waves for that very reason—they’re stable, clean, and efficient.

Now switch gears to communication systems. Whether you’re streaming Netflix, making a phone call, or even using Wi-Fi, those signals are being modulated on top of sine wave signals. Why again? Because sinusoids can be easily manipulated to carry information without distorting it, even across vast distances.

Here’s a quick breakdown of why it’s foundational:

Mathematical Simplicity: Sine waves make the math behind circuits and signals a lot easier to work with.
Fourier Analysis: Every complex signal can be broken down into multiple sinusoidal waves, which makes analysis and filtering possible.
Natural Behavior: Systems like capacitors and inductors naturally respond to sinusoids in predictable ways.

So yeah, the sine wave isn’t just some academic curve—it’s literally the blueprint of modern electrical and data transmission systems.

Mathematical Foundation and Wave Equation

The sinusoidal wave isn’t just a smooth curve—it has a precise mathematical form. The standard wave equation looks like this:

v(t) = Vm × sin(ωt + φ)

Each symbol in this equation tells a story:

v(t): The instantaneous value of the sine wave signal at time t.
Vm: The amplitude, or peak value of the wave—how high or low it goes.
ω: The angular frequency in radians per second. It relates to the number of oscillations per second via ω = 2πf.
t: Time, the independent variable—how the signal evolves.
φ: The phase angle, which shifts the wave left or right on the time axis.

Most signals are expressed in this sinusoidal waveform because it mirrors how real-world systems behave. However, it’s common to see an equivalent cosine form too:

v(t) = Vm × cos(ωt + φ)

Since sine and cosine are just phase-shifted versions of each other (by 90°), the choice between them depends on your reference point. Engineers often use sine waves by default unless a system’s response begins at its peak—then the cosine makes more sense.

Core Characteristics of a Sinusoidal Wave

Understanding a sinusoidal wave means breaking it down into its measurable properties. These characteristics are what make the sine wave signal a reliable foundation in alternating current (AC) systems.

Amplitude: This is the maximum value the wave reaches from the center (zero) line. It defines the strength of the signal.
Peak-to-Peak Value: It’s simply twice the amplitude. If a wave peaks at +10V and dips to -10V, its peak-to-peak value is 20V.
RMS Value (Root Mean Square): For a pure sine wave, this is Vm / √2. It represents the effective value—how much power the wave delivers.
Average Value: Over one full cycle, the average value of a pure AC waveform is zero. But over a half-cycle, it equals (2Vm) / π.
Time Period (T): The duration of one complete cycle of the wave, usually in seconds.
Frequency (f): Measured in Hertz (Hz), it tells how many cycles occur per second. It’s the inverse of the time period: f = 1/T.
Angular Frequency (ω): This links time and frequency mathematically. ω = 2πf shows how fast the wave oscillates in radians per second.
Phase Shift (φ): This represents how much the wave is offset horizontally. It’s measured in degrees or radians.
Time Shift: Instead of using phase in angles, you can express the shift in terms of time. For example, a shift of 90° at 60Hz equals 4.17 milliseconds.

Together, these characteristics define every point of a sinusoidal waveform, making it easy to analyze, simulate, and manipulate in real-world systems.

Graphical and Visual Analysis

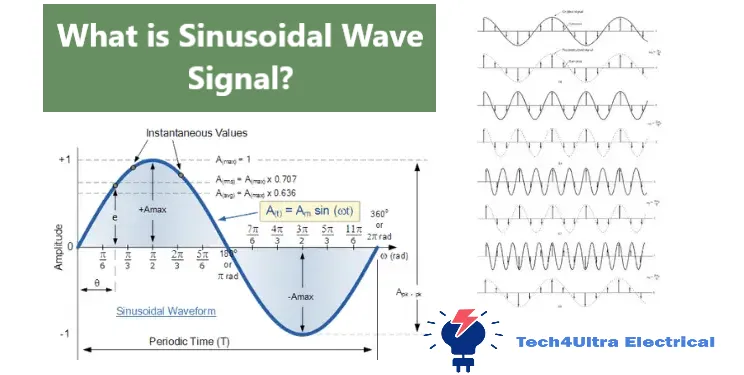
One of the best ways to understand a sinusoidal wave is by looking at its graph. A typical sine wave signal plotted over time creates a smooth, oscillating curve that repeats every cycle.

When plotting the waveform, the horizontal axis represents time (t), and the vertical axis shows the amplitude. The curve starts at zero, rises to a peak, falls back to zero, dips to a trough, and returns to zero—completing one full AC waveform cycle.

Key points to mark on the graph:

Zero Crossing: Where the wave crosses the time axis—these points represent moments of zero voltage or current.
Peak: The highest point of the wave—equal to the positive amplitude.
Trough: The lowest point—equal to the negative amplitude.

Adding annotations to the graph, such as labeling the time period (T), frequency (f), and phase shifts, helps visualize how the waveform behaves and interacts with other signals. Engineers often rely on these annotated plots to compare signals, diagnose timing issues, and ensure synchronization in alternating current (AC) systems.

Physical Interpretations and Real-World Analogs

The beauty of the sinusoidal wave lies in how naturally it appears in the physical world. Far from being just a mathematical function, the sine wave signal mirrors real-world phenomena in motion, sound, and electricity.

First up: uniform circular motion. Imagine a point moving in a perfect circle at constant speed. If you observe its vertical position over time, it traces a perfect sine wave. That’s where the term “sinusoidal” originates. The wave is the projection of circular motion onto a straight line.

Next, we have simple harmonic motion (SHM). Think of a pendulum or a spring moving back and forth. The displacement over time follows a sinusoidal waveform, showing how energy transfers smoothly between kinetic and potential forms. This is the core of so many natural and mechanical systems—oscillations, vibrations, and waves.

And then there are the everyday examples:

Sound waves: When a tuning fork vibrates, it produces air pressure variations that propagate as sine wave signals. Your ear interprets these as sound.
AC electricity: The voltage from your wall socket isn’t flat—it’s a sinusoidal wave. That’s why we call it alternating current (AC). It cycles smoothly between positive and negative voltages, ideal for energy transmission.

In short, sinusoidal waves are nature’s favorite pattern. Whether it’s sound, light, motion, or current, they show up everywhere—and that’s why understanding them isn’t just useful, it’s essential.

Applications in Engineering and Physics

Sinusoidal wave signals are more than academic—they’re essential tools in the real world. From powering your home to transmitting your voice over a phone call, the sine wave drives countless technologies in engineering and physics.

Let’s start with AC signal generation and transmission. In power systems, alternating current (AC) is generated as a sinusoidal waveform because it’s efficient to produce and easy to step up or down using transformers. This makes it ideal for long-distance energy transmission, reducing power loss and improving system stability.

In circuit analysis, engineers use phasor representation to simplify calculations involving sine wave signals. A phasor converts a time-dependent wave into a complex number in the frequency domain, making it easier to analyze voltages and currents in AC circuits—especially when dealing with inductors, capacitors, and resistors.

Then there’s communication. Nearly every form of modern communication—Wi-Fi, radio, cellular networks—relies on modulating information onto sinusoidal carriers. By changing amplitude, frequency, or phase (AM, FM, and PM), data is embedded within sine waves and transmitted over the air.

Even in filtering systems, understanding the behavior of sinusoidal waveforms helps in designing circuits that isolate or block certain frequencies. Low-pass, high-pass, and band-pass filters all rely on predictable sine wave responses.

So, whether you’re an electrical engineer, physicist, or just curious, grasping the role of AC waveforms opens the door to understanding how the world really works—one cycle at a time.

Advanced Concepts and Signal Analysis

Once you’re comfortable with the basics of a sinusoidal wave, it’s time to explore how these waves unlock powerful tools in advanced engineering and physics. One of the most revolutionary ideas? The Fourier series.

The Fourier series allows us to break down any periodic signal—even complex, jagged ones—into a sum of multiple sine wave signals at different frequencies and amplitudes. These additional sine waves are called harmonics, and they represent the signal’s harmonic content. This concept is the foundation of signal processing, audio compression, image filtering, and more.

Another essential topic is calculus with sine waves. When you differentiate a sine wave, you get a cosine wave (and vice versa, with a negative sign). This has real-world consequences—such as velocity being the derivative of position in simple harmonic motion. Integration, on the other hand, accumulates the area under the curve, which is crucial in energy and signal power analysis.

Now let’s talk about multi-phase systems. In electrical power distribution, three-phase systems use three sinusoidal waveforms that are 120 degrees out of phase from each other. These phase relationships balance loads, reduce vibration in motors, and improve efficiency in industrial applications. For instance, when analyzing a three-phase motor, engineers use phasor diagrams to visualize the timing between waveforms and optimize performance.

So whether it’s filtering noise from an audio signal, analyzing signal phase in a communication system, or managing power in a factory, mastering these advanced behaviors of the AC waveform gives you a whole new level of control and insight.

Practical Example and Calculation Section

Let’s walk through a step-by-step example to bring the sinusoidal wave to life using actual numbers. Suppose we have a voltage signal described by the equation:

v(t) = 170 × sin(2π × 60 × t)

This is a typical household alternating current (AC waveform) in many regions. Here’s how to interpret it:

Amplitude (Vm) = 170V — This is the peak voltage.
Frequency (f) = 60Hz — This means the signal completes 60 cycles every second.
Angular Frequency (ω) = 2π × 60 = 377 rad/s

Now, let’s calculate the RMS value:

Vrms = Vm / √2 = 170 / √2 ≈ 120V

This is the effective voltage that powers household devices. It’s what your wall outlet delivers, even if the peak is technically 170V.

Waveform Shape: Since it follows a standard sine function with no phase shift (φ = 0), it starts at zero, peaks at 170V, dips to -170V, and repeats every 1/60 seconds (≈16.67 ms).

This simple example shows how sine wave signals are used in real-world AC applications—and how we calculate meaningful values like RMS and frequency from just one equation.

Watch Also: Seebeck Effect: Definition, Formula and Applications

Common Misconceptions and Clarifications

Even though the sinusoidal wave is a staple in electrical systems, there are still some widespread misconceptions that trip people up. Let’s clear a few of them up:

RMS vs. Average Value: Many assume these are the same. They’re not. The RMS value measures the effective power of the sine wave signal, while the average over a full AC waveform cycle is zero. Only the average over half a cycle gives a meaningful value.
Sine vs. Cosine: People often think they’re completely different waves. In truth, they’re the same shape but offset in time. A cosine wave leads a sine wave by 90° (π/2 radians).
Amplitude vs. Peak-to-Peak: It’s easy to confuse these. Amplitude is the height from zero to the peak. Peak-to-peak is double that—measuring from the wave’s highest point to its lowest.

Getting these basics straight helps you avoid major calculation errors in analyzing AC waveforms and designing circuits.

Conclusion

To wrap it up, here’s what you need to remember:

Sinusoidal wave signals are smooth, repeating curves defined by amplitude, frequency, and phase.
The standard AC waveform follows the form v(t) = Vm × sin(ωt + φ).
RMS values reflect real-world power, while peak-to-peak values show the full voltage swing.

Why are sine waves preferred in alternating current (AC) analysis? Because they simplify calculations, reflect natural system behavior, and support efficient energy transmission and communication. Mastering them is a must for anyone working with signals, circuits, or electrical systems.

FAQs

How do you read a sinusoidal wave?

Reading a sinusoidal wave means interpreting its key features—amplitude, frequency, phase, and time. Start by identifying the zero crossings where the wave intersects the time axis. Then, look for the peaks and troughs to determine the amplitude. Measure the time between two peaks to find the period, and use f = 1/T to get the frequency. Understanding the phase shift helps you see how it aligns (or misaligns) with other signals.

What is the theory of a sinusoidal signal?

The theory behind a sinusoidal signal is rooted in mathematics and physics. It describes a wave that follows the function v(t) = Vm × sin(ωt + φ). This model applies to systems experiencing simple harmonic motion or alternating current (AC). The sinusoid is not just a curve—it represents the fundamental behavior of periodic signals in natural and engineered systems. It’s also the building block of the Fourier series, which means every periodic signal can be expressed as a sum of sine waves.

What is the waveform of a sinusoidal signal?

The waveform of a sinusoidal signal is a smooth, continuous curve that oscillates above and below a central axis in a repeating pattern. It has a well-defined amplitude, frequency, and phase. This shape is symmetric and periodic, making it ideal for power systems and signal processing. A single cycle consists of a rise to a peak, fall through zero to a trough, and return to zero.

What is the importance of understanding sinusoidal waves?

Understanding sinusoidal waves is essential in electrical engineering, physics, and communications. They’re the foundation of AC waveform analysis, signal transmission, and circuit behavior. Knowing how they work helps diagnose signal interference, optimize energy efficiency, and design reliable systems. Whether you’re building a speaker or analyzing a power grid, the sine wave signal is at the core of your success.

What makes a wave sinusoidal?

A wave is considered sinusoidal if it follows the form v(t) = Vm × sin(ωt + φ). It must have a smooth, repetitive pattern that oscillates symmetrically around a central axis. This predictable shape is what makes it ideal for AC waveform generation, system modeling, and signal analysis.

How do sine waves differ from square or triangular waves?

Sine wave signals are smooth and continuous. In contrast, square waves switch abruptly between high and low states, and triangular waves have linear, angled rises and falls. While sine waves are used in power and communication systems for their efficiency and harmonic simplicity, square and triangular waves are often used in digital signals and timing circuits but can produce more noise and higher harmonic content.

What is the significance of phase angle?

The phase angle (φ) tells you how much a sinusoidal wave is shifted horizontally from a reference point. It’s essential in multi-signal systems like three-phase power or signal synchronization. When multiple AC signals interact, knowing their phase differences helps predict interference, amplification, or cancellation effects—making it critical for engineering accuracy.

Sinusoidal Wave Signal: Definition and Examples

Contents