Ever looked at Watts Law and wondered, “Why should I care about this power equation?”
Many beginners—and even tech-savvy folks—struggle to fully grasp the power voltage current relationship, even though it’s the foundation of every electrical system.

In this article on the Tech4Ultra Electrical website, I’ll break down Electrical power concepts into simple, relatable steps. You’ll understand how the Power formula works and why mastering it gives you real control over how electricity flows in your projects and devices.

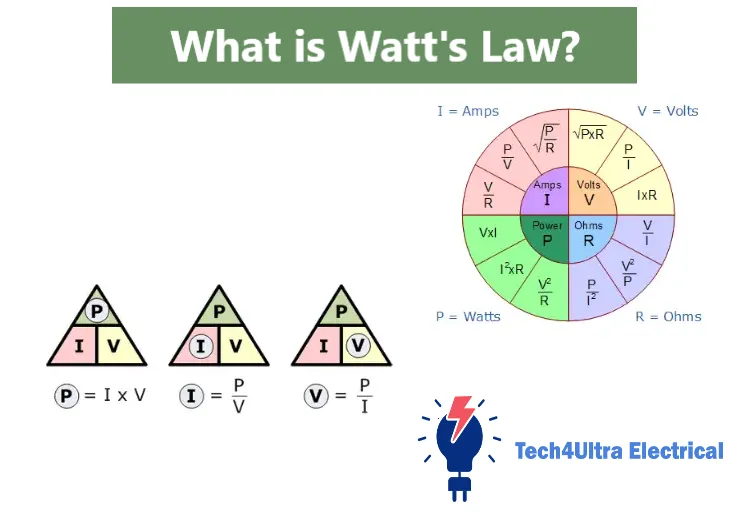
What Is Watts Law?

Simple Definition

Watts Law is the formula that explains how electrical power is related to voltage and current. Simply put, it states that power (P) equals voltage (V) multiplied by current (I):

P = V × I

This is the core Power formula that tells you how much energy a device consumes or generates over time. Whether you’re working with a phone charger or a heavy industrial motor, this formula applies universally.

Historical Background (James Watt and Energy Concepts)

The law is named after James Watt, the Scottish inventor and mechanical engineer who revolutionized the steam engine. His work in the 18th century helped define the modern concept of power as the rate of doing work or converting energy. The unit of power, the “watt,” honors his legacy.

Before Watt, energy was a fuzzy concept. After him, we had a way to measure it in real-world applications.

Why It Matters in Practical Engineering

Understanding the power voltage current relationship is essential in any electrical system design. Whether you’re sizing a solar panel system or choosing a resistor, using Watts Law helps avoid overheating, inefficiency, and component failure.

It’s not just theory—it’s everyday electrical safety and efficiency, built on one clear formula.

Watts Law Formula Breakdown

Formula: P = V × I

At the heart of Watts Law lies one powerful equation:

P = V × I

This Power formula tells us how much electrical power is consumed or generated in a circuit. To apply it properly, you need to understand what each symbol means and the correct unit for each.

Explanation of Each Term (P, V, I) with SI Units

P (Power) is the rate at which energy is used or produced. It’s measured in watts (W). 1 watt equals 1 joule per second.
V (Voltage) is the electrical potential difference between two points. It’s measured in volts (V). Think of it as the “push” that drives electric current.
I (Current) is the flow of electric charge. It’s measured in amperes (A), often just called “amps.” More current means more electrons flowing through the wire.

When to Use This Formula

Use the power voltage current relationship when you need to:

Calculate the power consumption of any device (like a light bulb or phone charger).
Design circuits and choose components with the right ratings.
Troubleshoot electrical problems—like figuring out if a power supply is strong enough.

Where there’s voltage and current, Watts Law is your go-to formula for getting answers.

How Watts Law Relates to Ohm’s Law

Combining Ohm’s Law with Watts Law

If you’ve already met Ohm’s Law (V = I × R), you’re halfway to mastering power calculations. By combining it with Watts Law, you unlock two powerful variations of the Power formula that let you calculate electrical power without needing both voltage and current at the same time.

Derived Forms: P = I²R and P = V²/R

P = I² × R: Use this when you know the current (I) and resistance (R). The higher the current or resistance, the more power gets converted into heat—useful for designing heating elements or checking for overheating in circuits.
P = V² ÷ R: Use this when you know the voltage (V) and resistance (R). This version is perfect when you’re dealing with a known voltage source like a battery or power supply.

These forms all stem from the basic power voltage current relationship. Knowing how to switch between them is a skill every engineer or DIY enthusiast should have.

Real-Life Circuit Examples Using Both Laws

Imagine a 12V car battery powering a 6-ohm headlight. Using P = V² ÷ R, you get P = (12)² ÷ 6 = 144 ÷ 6 = 24 watts.
Or take a 2A current flowing through a 5-ohm resistor in a heater. P = I² × R = (2)² × 5 = 4 × 5 = 20 watts.

In both cases, Watts Law gives you a clear picture of energy use, while Ohm’s Law helps you understand how the voltage, current, and resistance are connected.

Calculating Power in DC vs. AC Circuits

Differences in AC and DC Power Calculation

In a DC circuit, power calculation is straightforward. You just use the classic Watts Law formula: P = V × I. The voltage and current are constant, so what you calculate is exactly what you get—electrical power is easy to predict.

In AC circuits, it’s not that simple. Because voltage and current can vary over time (they alternate), calculating Power depends on more than just V and I. That’s where things like power factor come in.

Real, Reactive, and Apparent Power

Real Power (P): This is the actual usable power, measured in watts (W). It does real work—like lighting a bulb or powering a motor.
Reactive Power (Q): Measured in VARs (volt-amp reactive), this power flows back and forth due to inductors or capacitors. It doesn’t do useful work but affects the system’s capacity.
Apparent Power (S): This is the combination of both, measured in VA (volt-amperes). It’s the total power supplied to the circuit.

The triangle formed by these three types of power helps you visualize what’s really happening in an AC system.

Power Factor and Its Effect

The Power factor is the ratio of real power to apparent power. A perfect power factor is 1.0, meaning all the supplied power is being used effectively.

If your power factor is low (say 0.7), you’re wasting energy—something no engineer or business wants. Correcting power factor can mean big savings on electric bills and better performance from your system.

In AC circuits, the power voltage current relationship must include these factors to get an accurate picture of energy flow.

Watts Law Examples and Step-by-Step Calculations

DC Example with Solution

Let’s say you’re working with a simple DC circuit that has a voltage of 9 volts and a current of 2 amps. How much electrical power does it consume?

Given:

V = 9 volts
I = 2 amps

Using Watts Law formula:

P = V × I = 9 × 2 = 18 watts

The device consumes 18 watts of power. Simple and clear.

AC Example with Power Factor

Now take an AC circuit with a voltage of 120V, a current of 10A, and a power factor of 0.8.

Given:

V = 120 volts
I = 10 amps
Power factor = 0.8

Real Power (P) = V × I × Power Factor

P = 120 × 10 × 0.8 = 960 watts

So the actual usable power here is 960 watts. This shows how the power voltage current relationship gets adjusted in AC systems due to phase shift.

Common Mistakes and How to Avoid Them

Ignoring units: Always double-check that you’re using volts, amps, and ohms correctly. Mixing milliamps with amps will throw off your entire result.
Forgetting the power factor: In AC calculations, skipping the power factor leads to overestimated power usage.
Wrong formula: Use the correct version of Watts Law depending on the values you have (like P = I²R if you don’t know voltage).
Not checking circuit type: Always confirm whether you’re dealing with DC or AC. They’re not interchangeable when it comes to applying Power formula.

Mastering these examples gives you real confidence in applying Watts Law accurately, whether you’re fixing a small device or planning a full electrical setup.

Applications of Watts Law in Everyday Devices

Light Bulbs, Heaters, Motors, Inverters

Watts Law isn’t just for textbooks—it’s working behind the scenes in almost every device you use.

Light Bulbs: When you see a bulb labeled “60W,” that’s its electrical power. If it runs on 120V, the current drawn is I = P ÷ V = 60 ÷ 120 = 0.5A. That’s power voltage current relationship in action.
Heaters: Electric heaters use high current. Knowing how much power they draw (say, 1500W) helps you choose the right wire and breaker size—again, straight from the Power formula.
Motors: Motors convert electrical power into mechanical motion. If the input is too high or too low, it affects performance and efficiency—understanding Watts Law helps prevent overloading.
Inverters: These convert DC to AC, and proper power rating ensures they won’t trip or overheat. Technicians use Watts Law to match devices to the inverter’s capacity.

How Technicians and Engineers Apply This Law

In the real world, professionals rely on Watts Law daily:

To size fuses and circuit breakers.
To prevent equipment failure from overcurrent.
To balance loads in power distribution systems.

Whether it’s a home appliance or an industrial panel, understanding this simple formula keeps systems safe, efficient, and reliable.

Power vs. Energy: The Difference Explained

E = P × t Explained

Here’s a common confusion: electric power isn’t the same as energy. Think of Watts Law as telling you how fast you’re using energy. To find out how much total energy was used, you need this formula:

E = P × t

Where:

E is energy in watt-hours (Wh)
P is power in watts (W)
t is time in hours (h)

Example Calculation of Energy Usage

If a 100-watt light bulb is on for 5 hours, the energy used is:

E = 100 × 5 = 500 Wh

That’s half a kilowatt-hour (kWh), the unit your electricity bill measures.

Relevance in Electricity Bills

Your electric company charges you based on energy—not just how much power a device uses, but for how long it runs. A heater that draws 2000W might not seem like much, until it runs for 10 hours. That’s 20,000 Wh, or 20 kWh—definitely noticeable on your bill.

Understanding the power voltage current relationship helps, but combining it with time lets you see the full picture: how power becomes energy.

Watch Also: Transformer Efficiency Explained: Calculation, Losses, and Optimization Strategies

Interactive Section: Practice Questions & Quiz

Multiple-Choice Questions

What does Watts Law state?
A) V = I × R
B) P = V × I
C) I = V ÷ R
Answer: B – This is the core Power formula.
What is the SI unit of electrical power?
A) Joule
B) Ampere
C) Watt
Answer: C – Power is measured in watts.
Which form of power does not do actual work?
A) Real Power
B) Reactive Power
C) Apparent Power
Answer: B – Reactive power just circulates in the system.

Numerical Question

A circuit has 240V and draws 5A. How much power does it use?

Solution: P = V × I = 240 × 5 = 1200 watts

This shows the practical use of the power voltage current relationship.

Conclusion

By now, you’ve seen how Watts Law isn’t just theory—it’s the foundation of how we understand and control electrical power. Whether you’re calculating the load on a simple light bulb or designing complex systems with motors and inverters, mastering the power voltage current relationship gives you real-world electrical confidence.

Remember, the core Power formula—P = V × I—is the key to almost every power calculation you’ll ever make. And when combined with Ohm’s Law and time, it becomes even more powerful.

Next time you look at your electricity bill, plug in a device, or troubleshoot a circuit, you’ll know exactly what’s happening behind the scenes. That’s the power of understanding power.⚡

FAQs

What is the Watts law triangle?

The Watts Law triangle is a simple visual tool that helps you remember the Power formula. It’s a triangle divided into three parts with P (Power) on top, and V (Voltage) and I (Current) at the bottom. Cover the one you’re solving for, and you’ll know which formula to use: P = V × I, V = P ÷ I, or I = P ÷ V.

What is an example of the Watts law?

If a fan runs on 120 volts and uses 2 amps of current, the electrical power it consumes is:
P = V × I = 120 × 2 = 240 watts.
This is a classic example of applying the Watts Law in real life.

What are the 3 formulas in Watts law?

The three core formulas based on the power voltage current relationship are:

P = V × I (Power)
V = P ÷ I (Voltage)
I = P ÷ V (Current)

These allow you to solve for any missing value when two others are known.

What is the formula for Watts example?

Here’s a practical example: A laptop charger supplies 19 volts and 3.42 amps. To find the power:
P = V × I = 19 × 3.42 = 64.98 watts
That’s how much power the charger provides using Watts Law.

How to calculate power formula?

To calculate electric power, use Watts Law: P = V × I, where P is power in watts, V is voltage in volts, and I is current in amps.

What are the 3 equations for power?

The three core forms of Watts Law are:
P = V × I,
P = I² × R,
P = V² ÷ R

How to find wattage?

Wattage (power in watts) is found using the formula P = V × I. Multiply the voltage by the current flowing through the device.

What is an example of watts?

If a heater uses 230V and draws 5A, its power is P = 230 × 5 = 1150 watts. That’s how much energy it uses per second.

What is the 3 formula of power?

They are the same as earlier:
P = V × I, P = I² × R, and P = V² ÷ R. Use the one that fits the values you have.

What are the 4 equations for power?

Along with the 3 basic forms, add E = P × t, which calculates energy. It’s how power and time combine to give energy used.

How do you solve 3 powers?

If you’re solving powers like 3³, it means 3 multiplied by itself 3 times: 3 × 3 × 3 = 27.

How to calculate 3 power 3?

It’s the same: 3³ = 27. This is called exponentiation or raising a number to a power.

What is Power of 4 called?

Power of 4 is written as x⁴ and means x × x × x × x. It’s called “x raised to the 4th power.”

How to calculate power value?

Use Watts Law. If you have voltage and current, multiply them: P = V × I. If you have resistance, use the alternate forms.

What are the 7 laws of exponents?

The 7 laws include product, quotient, power of a power, zero exponent, negative exponent, and more. These are algebraic, not specific to electric power.

What is 4 cubed in maths?

4³ means 4 × 4 × 4 = 64. This is called “4 cubed” because it’s raised to the 3rd power.

What is 2 raised to 0?

Any number (except 0) raised to the power of 0 equals 1. So, 2⁰ = 1.

Contents