I’ve always found it puzzling how something as tiny as an atom could behave in ways that defy classical physics. But everything started making sense when I discovered the Schrödinger wave equation.

In this article on the Tech4Ultra Electrical website, I’ll break down how this fundamental equation reshaped quantum mechanics, and how the concept of the wave function helps us understand the bizarre behavior of particles at the quantum level. If you’ve ever wondered what lies behind the curtain of atomic behavior, this is your starting point. Let’s dive in.

What is the Schrödinger Equation?

I still remember the first time I came across the Schrödinger wave equation in a dusty physics textbook. I skimmed past it, thinking it was just another complex formula. Big mistake. That equation was a door — a key to understanding the very foundation of quantum mechanics.

At its core, the Schrödinger equation isn’t just math. It’s the backbone of quantum physics — the equation that tells you how a wave function evolves over time. And in the quantum world, that wave function is everything. It describes where a particle might be, how it might behave, and how likely it is to show up in a certain place.

Let me tell you what I wish someone had told me back then: the Schrödinger equation is not about certainties. It’s about probabilities. That was mind-blowing. In classical mechanics, you know where a ball is and where it’s going. In quantum mechanics, you only know where it might be — and that’s where the wave function steps in.

Here’s what the time-dependent Schrödinger equation looks like:

iħ ∂ψ/∂t = Ĥψ

Sounds intense, right? But don’t worry — the real beauty lies in what it means:

ψ is the wave function, which holds all the information about a system.
ħ is the reduced Planck’s constant.
Ĥ is the Hamiltonian operator, representing the total energy of the system.
The equation basically tells us how ψ changes over time.

Why is this important?

Because nothing else in quantum mechanics really works without it. You want to understand atomic orbitals? Schrödinger equation. Electron behavior in semiconductors? Schrödinger again. Heck, even quantum computing wouldn’t exist without this foundation.

So, if you’re serious about understanding the quantum world, this is where it begins. Take your time with it. I didn’t at first — and I paid for it with confusion and frustration. But once it clicked, it changed everything.

Understanding the Wave Function in Quantum Theory

Physical interpretation of the wave function

One of the biggest misconceptions I had early on was thinking the wave function represented a physical wave like sound or water. It’s not. In quantum mechanics, the wave function — usually denoted as ψ — is more like a code that contains all the possible outcomes of a quantum system. It doesn’t show what is happening, but what could happen, and with what likelihood.

Real vs. imaginary components

What confused me most was that the wave function often contains imaginary numbers. How can something imaginary describe real particles? Here’s the trick: it’s not the function itself we observe, but the square of its absolute value, |ψ|², which is always a real number. That’s the part with physical meaning — it tells you the probability density.

Role in probability theory

The Schrödinger wave equation gives us the time evolution of the wave function, but to actually predict outcomes, we rely on probability. The value of |ψ(x,t)|² tells us the likelihood of finding a particle at a specific point in space and time. This is why the wave function is so central — it’s our only way of making statistical predictions in the quantum world.

Mathematical Formulation of the Schrödinger Equation

General form of the equation

The beauty of the Schrödinger wave equation lies in its elegant form. It’s usually written as:

iħ ∂ψ/∂t = Ĥψ

This is the time-dependent form, where ψ is the wave function, ħ is the reduced Planck’s constant, and Ĥ (the Hamiltonian) represents the total energy of the system. If we assume the system doesn’t change with time, the equation simplifies to the time-independent version:

Ĥψ = Eψ

Here, E is the energy eigenvalue, and solving this gives us quantized energy levels — a revolutionary idea in quantum mechanics.

Introduction to operators (Hamiltonian, Laplacian)

Operators in quantum mechanics act on the wave function to extract physical information. The Hamiltonian operator (Ĥ) includes two parts: kinetic energy and potential energy. The kinetic part often uses the Laplacian operator (∇²), which describes how a function curves in space. For a single particle in 3D space, the kinetic energy operator looks like this:

−(ħ²/2m)∇²

When you apply this to the wave function, you’re essentially measuring how “wavy” it is — a clue to the particle’s momentum and energy.

Constants involved (Planck’s constant, etc.)

At the heart of the equation is Planck’s constant (h), or more precisely, the reduced version ħ = h/2π. It’s tiny — about 1.054 × 10⁻³⁴ Js — but it defines the scale at which quantum effects dominate. Another constant often present is the particle’s mass (m), especially in the kinetic energy term. Without these constants, the entire framework of the Schrödinger wave equation would fall apart.

Types of Schrödinger Equations

Time‑Dependent Schrödinger Equation

The time-dependent Schrödinger equation is the full version of the Schrödinger wave equation, describing how the wave function changes over both time and space. It’s written as:

iħ ∂ψ(x,t)/∂t = Ĥψ(x,t)

This form is essential for systems where conditions vary with time — think of a particle in an oscillating field or changing potential. It gives you a complete picture of the quantum state at every moment. When I first saw it, it looked intimidating, but once I realized it’s like Newton’s laws for quantum mechanics, it started to click.

Time‑Independent Schrödinger Equation

When the system has no time-varying forces — like an electron in a stable atom — we can simplify things. The time-independent Schrödinger equation drops the time term and focuses on spatial behavior only:

Ĥψ(x) = Eψ(x)

This is the version used to find the allowed energy levels in atoms, molecules, and even quantum wells. It’s what gave us the famous orbitals of hydrogen and the concept of quantized energy. Solving this version helped me understand why electrons don’t spiral into the nucleus — they’re “locked” in stable, probabilistic states defined by their wave functions.

Mathematical differences and applications

Mathematically, the key difference is that the time-dependent form involves partial derivatives with respect to time, while the time-independent form does not. The time-dependent equation is used for dynamics; the time-independent for stationary states.

In application, both are powerful. The time-dependent version is crucial for quantum computing, tunneling phenomena, and wave packet evolution. The time-independent version dominates in quantum chemistry and atomic physics — especially when predicting spectral lines and stable states.

Derivation of the Schrödinger Equation

Classical energy analogy

To make sense of the Schrödinger wave equation, it helps to start with something familiar: classical mechanics. In classical terms, the total energy (E) of a particle is the sum of kinetic and potential energy:

E = (p² / 2m) + V

Here, p is momentum, m is mass, and V is potential energy. Schrödinger wanted to translate this relationship into a version that works with wave functions — a cornerstone of quantum mechanics.

Operator substitution

This is where things get quantum. In quantum mechanics, we don’t use energy and momentum as plain variables. Instead, we substitute them with operators that act on the wave function:

Energy: E → iħ ∂/∂t
Momentum: p → −iħ ∇

These substitutions come from wave theory and the de Broglie hypothesis, which links particles and waves. When applied correctly, they allow us to describe particles not just as objects, but as evolving waves.

Step-by-step derivation

Start with the classical total energy: E = p² / 2m + V
Substitute p and E with their quantum operator forms:

iħ ∂ψ/∂t = [−(ħ² / 2m)∇² + V]ψ

This is the time-dependent Schrödinger wave equation. The left side represents the system’s energy evolution over time, and the right side contains the Hamiltonian operator acting on the wave function.

I remember the “aha!” moment when I saw how cleanly classical mechanics could be adapted with a little operator magic. Suddenly, quantum mechanics didn’t feel like a mystery — it felt like a logical next step.

Physical Interpretation and Probability

Born interpretation

When I first learned about the wave function, I kept asking: “What does it mean physically?” The answer came from Max Born, who proposed that the square of the wave function — |ψ(x,t)|² — represents a probability density. In simple terms, it tells us the likelihood of finding a particle at a particular place and time. This is now known as the Born interpretation, and it turned the abstract math of the Schrödinger wave equation into something measurable.

Normalization of the wave function

Since |ψ|² gives probabilities, we need to ensure that the total probability over all space is 1. That’s where normalization comes in. If your wave function isn’t normalized, the math might work, but the physics doesn’t. You normalize by integrating |ψ(x)|² over all space and adjusting ψ so that the result equals 1.

Probability density functions

The function |ψ(x)|² is what we call a probability density function in quantum mechanics. It doesn’t tell you where the particle is, but where it’s most likely to be. This idea blew my mind — it was a shift from certainty to statistical expectation. And that’s one of the biggest leaps when stepping from classical to quantum thinking.

Applications in Quantum Mechanics

Particle in a one-dimensional box

This was the first system I solved using the Schrödinger wave equation, and honestly, it changed how I viewed physics. Imagine a particle trapped in a box where the walls are infinitely high — it can’t escape. Solving the time-independent Schrödinger equation for this system gives quantized energy levels:

Eₙ = (n²π²ħ²) / (2mL²)

Here, n is an integer (1, 2, 3…), m is the particle’s mass, and L is the width of the box. The wave function forms standing waves, and the particle’s position becomes probabilistic — a clear sign you’re in the world of quantum mechanics.

Quantum harmonic oscillator

This is a step up in complexity. Think of a particle oscillating around a stable point — like a mass on a spring. The wave functions for this system are not just sine waves but involve Hermite polynomials and Gaussian envelopes. Yet, the energies remain quantized:

Eₙ = (n + 1/2)ħω

This half-quantum of energy, (1/2)ħω, is called the zero-point energy. Even at absolute zero, the particle still has motion. That concept shook me — nothing is ever truly at rest in the quantum world.

Hydrogen atom

Solving the Schrödinger wave equation for the hydrogen atom is where the theory really proves itself. You get discrete energy levels that match the spectral lines seen in experiments. The wave functions become 3D shapes — the famous atomic orbitals. This is where quantum mechanics gives us a model that classical physics simply can’t.

Additional modern applications

Quantum computing: The behavior of qubits — the building blocks of quantum computers — is governed by the Schrödinger equation. Superposition and entanglement are direct consequences of wave function behavior.
Semiconductors: Devices like transistors and LEDs work because we understand how electrons move through materials, thanks to solutions of the Schrödinger equation.
Quantum tunneling: Particles can pass through potential barriers they shouldn’t, classically. This principle powers technologies like the scanning tunneling microscope and tunnel diodes.

Each of these applications shows how this single equation — once considered purely theoretical — has transformed into a tool that powers modern technology. For me, it took quantum physics from a textbook concept to something I saw all around me.

Common Misconceptions and Clarifications

Misunderstandings around imaginary numbers

One of the first things that tripped me up was the use of imaginary numbers in the wave function. I thought, “How can imaginary components describe something real?” But here’s the catch: we never measure the wave function directly. What we observe is its square modulus, |ψ|², which is always a real number. The imaginary part is essential for describing how the system evolves over time — without it, the math just doesn’t work.

Confusion between classical and quantum mechanics

Another big misconception is trying to apply classical logic to quantum mechanics. In classical physics, everything is deterministic. But the Schrödinger wave equation tells us what could happen, not what will happen. The idea that particles can be in multiple states at once (superposition) just doesn’t fit into classical thinking. You have to accept uncertainty — and embrace probability — to truly understand the quantum world.

Visual Aids and Interactive Simulations

Wave Function Visualization

Sometimes, all the math in quantum mechanics becomes easier to grasp with a good picture. Below is a simple graph showing the probability density |ψ(x)|² for a particle in a one-dimensional box (n=1):

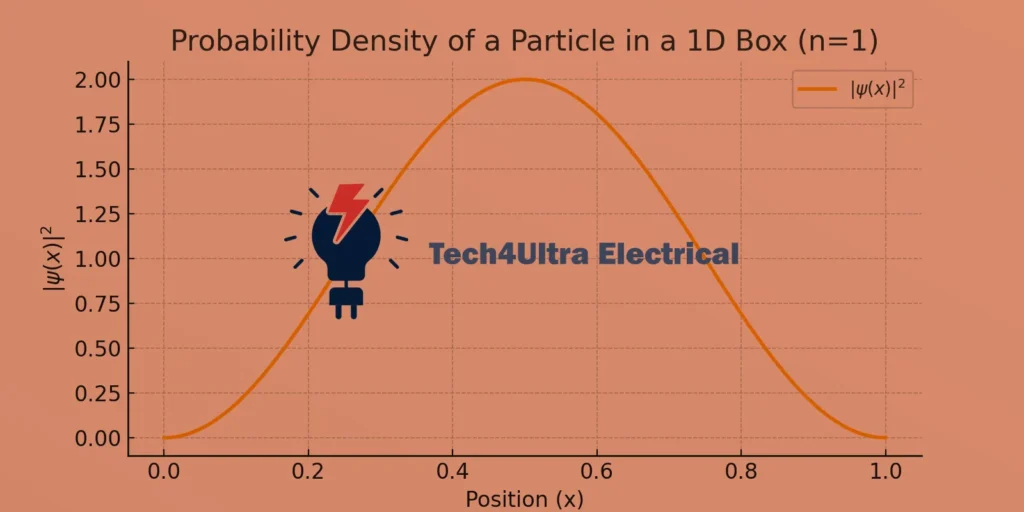
Interactive Simulation (external resource)

To see the wave function in action, check out this interactive simulation from PhET:

Quantum Tunneling and Wave Packets – PhET Interactive Simulation

Simple Python Script: Plotting a 1D Box Wave Function

Here’s a basic Python script using matplotlib and NumPy to visualize the wave function:

import numpy as np
import matplotlib.pyplot as plt

# Constants
L = 1  # Length of the box
n = 1  # Quantum number
x = np.linspace(0, L, 1000)
psi = np.sqrt(2/L) * np.sin(n * np.pi * x / L)

# Plot
plt.plot(x, psi**2, label='|ψ(x)|²')
plt.title('Probability Density: Particle in a 1D Box')
plt.xlabel('Position (x)')
plt.ylabel('Probability Density')
plt.grid(True)
plt.legend()
plt.show()

Encourage students to modify the value of n and observe how the shape of the wave function changes. It’s a fun way to learn that each energy level corresponds to a different standing wave.

Watch Also: Sinusoidal Wave Signal: Definition and Examples

Conclusion

The Schrödinger wave equation is the cornerstone of quantum mechanics, offering a mathematical path to understanding particles at the smallest scales. Through the concept of the wave function, we shifted from certainty to probability, unlocking models like the particle-in-a-box, quantum harmonic oscillator, and hydrogen atom.

Whether it’s semiconductors, quantum computing, or spectroscopy, this equation continues to power real-world technologies. Understanding it means more than just solving equations — it’s about seeing how the universe operates beneath the surface.

If there’s one thing to take away: quantum weirdness has rules — and this equation writes them.

FAQs

What is Schrödinger’s wave equation and its derivation?

The Schrödinger wave equation is a fundamental equation in quantum mechanics that describes how the wave function of a quantum system evolves over time. Its derivation begins with classical energy expressions and replaces energy and momentum with operators. The result is a differential equation that predicts the behavior of quantum particles in different potential environments.

What is the interpretation of the Schrödinger equation?

The equation itself doesn’t give direct physical meaning, but the square of the wave function, |ψ|², provides a probability density. This tells us the likelihood of finding a particle in a given region of space and time. This interpretation, known as the Born interpretation, connects abstract mathematics to measurable outcomes.

What is ψ in Schrödinger’s equation?

The symbol ψ represents the wave function, a complex-valued function that encodes all the information about a quantum system. While ψ itself may be complex or even imaginary, the observable quantity is |ψ|², which gives the probability of a particle’s position or state.

What is the derivation of the wave equation?

To derive the Schrödinger wave equation, you start from the classical energy equation: E = p²/2m + V. Then, using operator substitution where E becomes iħ∂/∂t and p becomes −iħ∇, you transform this classical relation into a quantum one. This leads to the time-dependent equation: iħ∂ψ/∂t = Ĥψ, which is the foundation of non-relativistic quantum mechanics.

What is the wave equation explained?

The wave equation is a mathematical expression that describes how waves move through space and time. In its classical form, it’s used for sound waves, light waves, and water waves. In quantum mechanics, the Schrödinger wave equation is a specific kind of wave equation that applies to particles, treating them as wave-like entities. It predicts the evolution of the wave function, which holds all the possible outcomes for a quantum system.

What are the four types of waves?

Waves can be classified based on the medium and how they propagate. Here are the four primary types:

Mechanical waves: Require a medium (like air or water) to travel through. Examples include sound waves and seismic waves.
Electromagnetic waves: Do not require a medium and can travel through vacuum. Examples include light, X-rays, and radio waves.
Matter waves: Central to quantum mechanics, these describe particles behaving like waves, governed by the Schrödinger wave equation.
Transverse and longitudinal waves: A categorization based on motion — in transverse waves, particles move perpendicular to the wave direction (e.g., light); in longitudinal, they move parallel (e.g., sound).

What are all 7 waves?

The term “7 waves” usually refers to the seven types of electromagnetic waves in the electromagnetic spectrum. These waves differ by wavelength and frequency but all travel at the speed of light in a vacuum. They are:

Radio waves
Microwaves
Infrared radiation
Visible light
Ultraviolet radiation
X-rays
Gamma rays

What are the 7 main types of waves?

In a broader sense, including both mechanical and electromagnetic categories, the 7 main types of waves can be listed as:

Sound waves (mechanical, longitudinal)
Water waves (mechanical, surface)
Seismic waves (P and S types)
Radio waves
Microwaves
Light waves (visible part of the EM spectrum)
X-rays and Gamma rays

How to explain waves?

A wave is a repeating disturbance or vibration that travels through space or a medium, transferring energy without permanently moving matter. You can think of it like a ripple in water — the water doesn’t move far, but the ripple (the energy) does. In quantum mechanics, particles themselves behave like waves, described by a wave function that evolves according to the Schrödinger wave equation.

Contents